The relational model is based on the principles of the relational algebra. The relational algebra is a collection of operators that operate on relations. Each operator takes one or two relations as input and produces the new relation as its output.

The lists of operators that have been defined as relational operators with detailed explanation are mentioned in this chapter.

2.1 Restrict Operator

The restrict operator extracts the specified tuples or rows from the given relation based on a condition. The following diagram shows how restrict operator can extract the specified tuples or rows from a given relation.

In the above diagram, the black colored rows represent the extracted rows from the relation by using the operator.

Consider an example of STUDENT table. It has attributes as ROLLNO, STUDNAME, AGE and GENDER.

The following table describes the columns of the STUDENT table.

The condition is to extract the tuples whose age is more than 25. The following table describes the relation.

2.2 Project Operator

The project operator is used to extract the specified attributes or columns from a given relation. The following diagram represents how project operator can extract specified attributes or columns from a given relation.

In the diagram, the black colored represent the extracted columns by using the project operator.

User can use the PROJECT operator it select some Age and STUDNAME from the STUDENT table. Apply the operator on the above mentioned STUDENT table. The output is as shown below:

2.3 Product Operator

The product operator joins the two relations such that every tuple of the first relation is matched with every tuple of the second relation. To be product compatible, the two relations must have common attribute. The following diagram shows the example of the product operator.

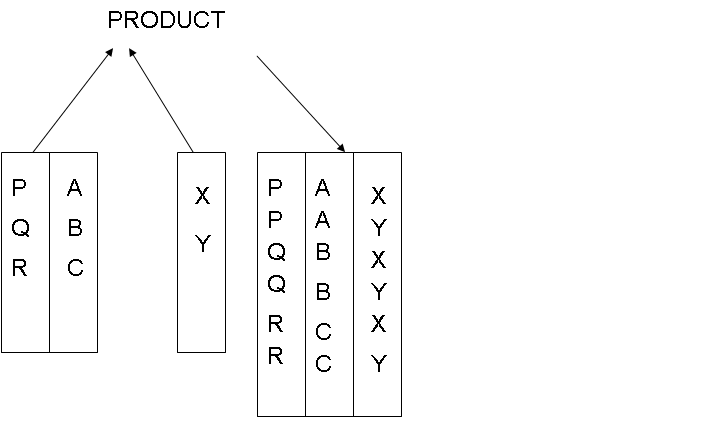
The product operator creates the Cartesian product between the two tables. Consider a TEACHER table which contains two attributes as T_CODE and NAME. Table BATCH contains BATCH_CODE and T_CODE. The T_CODE is the common attribute between the two tables.

TEACHER

BATCH

The following table lists the product of the TEACHER and BATCH tables with all the possible combinations of their tuples.

2.4 Union Operator

The union operator builds a relation from tuples appearing in either or both of the specified relations. The following diagram represents the union operator.

To be union compatible, the two tables must have same type of attributes. Consider the two tables as A and B.

A

B

The table A contains roll no and names of the students whose principle subject is computer science. Table B contains roll no and names of the students whose principle subject is mathematics. These tables are union compatible because they have the same type of attribute.

The following table shows the union operation on table A and B.

2.5 Intersect Operator

The intersect operator builds the relation containing tuples that appear in both the relations. The following diagram represents the intersect operator.

Consider table P and Q.

P

Q

Anthony is doing double major and hence his name appears in both the tables. An intersect operation on both the tables P and Q extracts the common rows to both the relation.

The following table shows the intersect result.

A INTERSECT B

2.6 Divide Operator

The divide operator takes two relations and builds another relation consisting of values of an attribute of one relation that match all the values in the other relation. The following diagram shows the working of the operator.

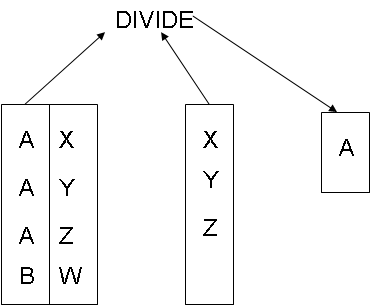
Consider an example of STUDENT. It contains the attributes as NAME and COURSECD. There is another table as COURSE, containing COURSECD attribute. It is common attribute in both the tables. Applying the divide operator on both the tables, the result will be the matching values of the relation, COURSE.

STUDENT

COURSE

RESULT OF DIVIDE

2.7 Difference Operator

The difference operator builds a relation of tuples appearing in the first but not in the second of the two specified relations. The following diagram represents the difference operator.

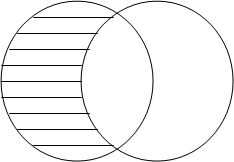
The following set of tables shows the difference operation on tables X and Y.

X

Y

X-Y

2.8 Join Operator

The join operator builds a relation from two specified relations. The relation consists of all possible combinations of tuples, one from each relation that satisfies the specified condition. The operation requires a common attribute. The following diagram represents the join operation.

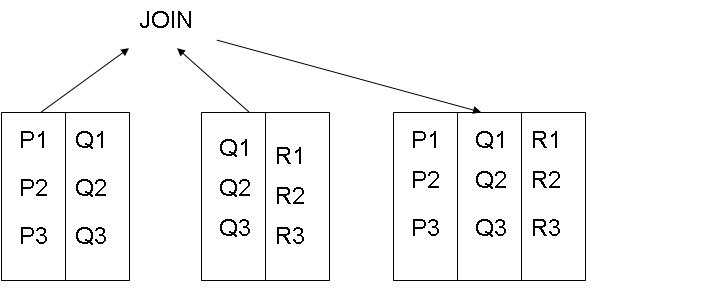
Consider an example of two tables as X and Y. Table X contains roll no and course codes. Table Y contains ID of teachers and the course code they teach. The join operation on these tables is as shown below:

X

Y

X JOIN Y